Pojam skupa

Skup

Skup je jedan od najosnovnijih pojmova u matematici. Skupovi imaju veliku ulogu u razumevanju i izučavanju matematike, ali i prirode i svakodnevnog života. Predmeti, stvari ili živa bića koja imaju nešto što im je zajedničko čine jedan skup.

Primer iz svakodnevnog života je skup učenika odeljenja V-1. Zajednička osobina svih učenika odeljenja V-1 je da svi idu u isto odeljenje pa tako svi oni predstavljaju skup učenika odeljenja V-1.

Primer jednostavnog skupa iz matematike bio bi skup jednocifrenih prirodnih brojeva i ovaj skup sadrži brojeve 1, 2, 3, 4, 5, 6, 7, 8 i broj 9. Zajedničke osobine brojeva ovog skupa su da su to jednocifreni i da su to prirodni brojevi.

Elementi skupova i obeležavnje

Skup jednocifrenih prirodnih brojeva obeležava se i zapisuje na sledeći način:

\(A=\{ 1, 2, 3, 4, 5, 6, 7, 8, 9 \}\)

Skupovi se obeležavaju velikim slovima latinice. Skup koji je dat u primeru iznad je skup A.

Elementi skupa A su jednocifreni prirodni brojevi, oni se zapisuju unutar vitičastih zagrada i odvajaju zarezima. Za svaki od brojeva unutar zagrada kažemo da pripada skupu A, odnosno da je element skupa A.

Za broj 5 možemo reći da pripada skupu A, a to se zapisuje na sledeći način:

\(5\in A\)

Broj 0 se na nalazi unutra zagrada datog skupa A i kažemo da 0 ne pripada skupu A ili da 0 nije element skupa A i to zapisujemo na sledeći način:

\(0\notin A\)

Zapisivanje skupova

Skupove možemo zapisati na nekoliko različitih načina. Neki od načina zapisivanja su:

Zapis skupa nabrajanjem elemenata:

\(S=\{ 1, 3, 5, 7, 9 \}\)

Čitamo: Skup S sadrži elemente 1, 3, 5,7 i 9.

Zapis skupa opisivanjem njegovih elemenata:

\(P=\{ x|x \in N~i~x\le 3\}\)

Čitamo: Skup P sadrži elemente x takve da su to prirodni brojevi manji ili jednaki broju 3.

Venov dijagram

Venov dijagram predstavlja grafički prikaz skupa. Na slici ispod vidimo skup koji je predstavljen zatvorenom linijom. Na spoljnoj strani linije upisuje se naziv skupa ili se skup obeležava velikim slovom latinice. Elementi se obeležavaju tačkama pored kojih stoji oznaka. Sve tačke koje se nalaze unutar zatvorene linije su elementi skupa, a sve tačke van zatvorene linije nisu elementi skupa.

Sa slike skupa prikazane Venovim dijagramom možemo oučiti i zapisati skup A:

\(A=\{ 2, 4, 6, 8 \}\)

Elementi skupa A nalaze se unutar zatvorene linije i zapisujemo:

\(\{ 2, 4, 6, 8 \} \in A\)

Brojevi 0 i 1 na Venovom dijagramu nalaze se izvan zatvorene linije i oni ne pripadaju skupu A, pa zapisujemo:

\(\{ 0, 1 \} \notin A\)

Broj elemenata skupa

Broj elemenata skupa predstavlja ukupan broj različitih elemenata skupa. Ako ponovo za primer uzmemo skup A čiji su elementi jednocifreni prirodni brojevi:

\(A=\{ 1, 2, 3, 4, 5, 6, 7, 8, 9 \}\)

Dati skup A ima 9 različitih elemenata pa je broj elemenata ovog skupa 9 i to se zapisuje:

\(n(A)=9\)

Broj elemenata datog skupa T je 2 jer postoje samo dva njegova različita elementa i to su brojevi 1 i 2.

\(T=\{ 1, 1, 2, 2, 2 \}\)

Prirodnih brojeva ima beskonačno mnogo pa je i broj elemenata skupa prirodnih brojeva N beskonačan.

\(N=\{ 1, 2, 3, 4... \}\)

Skupovi se mogu zapisati navođenjem elemenata između vitičastih zagrada. Ako za skup D između zagrada nije naveden ni jedan element kažemo da je skup prazan, a to se zapisuje kao:

\(D=\{ ~\}\) odnosno \(D=\varnothing \)

Jednakost skupova

Dva skupa su jednaka ako imaju iste elemente. Raspored kojim su zapisani elementi skupova nije bitan kao što nije bitno ni da li je jedan isti element u skupu zapisan više puta, na primer,

\(\{a,a,b,c \}=\{c,a,a,b ~\}\)

Podskup skupa

Skup A je podskup skupa B samo ako je svaki element A istovremeno i element B. Na slici je skup jednocifrenih prirodnih brojeva B i skup neparnih jednocifrenih prirodnih brojeva A.

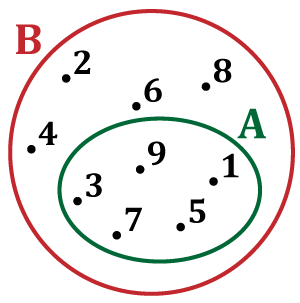
Svi elementi skupa A su istovremeno i elementi skupa B pa kažemo da je A podskup B i zapisujemo:

\(A \subset B\)

Prazan skup je podskup svakog skupa koji nije prazan:

\(\varnothing \subset \{a,b,c \}\)

Svaki skup je podskup samom sebi:

\(\{2,4,6 \} \subset \{2,4,6 \}\)